4回答

lewis

2020-06-16

已采纳

import * as tf from '@tensorflow/tfjs';
import * as tfvis from '@tensorflow/tfjs-vis';

window.onload = async () => {
const len = 40;
const xs = Array.from({ length: len }, (v, k) => (k - len / 2) / (len / 20));
const ys = xs.map(x => x ** 2);

tfvis.render.scatterplot(
{ name: 'x 的平方的数据' },
{ values: xs.map((x, i) => ({ x, y: ys[i] })) },
{
xAxisDomain: [-20, 20],
yAxisDomain: [0, 110]
}
);

const inputs = tf.tensor(xs);
const labels = tf.tensor(ys);

const model = tf.sequential();
model.add(tf.layers.dense({ units: 200, inputShape: [1], activation: 'sigmoid' }));
model.add(tf.layers.dense({ units: 1 }));
model.compile({ loss: tf.losses.meanSquaredError, optimizer: tf.train.adam(0.1) });

await model.fit(inputs, labels, {
epochs: 200,
callbacks: tfvis.show.fitCallbacks(
{ name: '训练过程' },
['loss'],
{ callbacks: ['onEpochEnd'] }
)
});

const output = model.predict(tf.tensor(xs));
const ysPred = output.dataSync();
tfvis.render.scatterplot(
{ name: '预测结果' },
{
values: [
xs.map((x, i) => ({ x, y: ys[i] })),
xs.map((x, i) => ({ x, y: ysPred[i] })),
],
series: ['原始数据', '预测数据']
},
{
xAxisDomain: [-20, 20],
yAxisDomain: [0, 110]
}
);
};

这是我写的代码，拿去参考一下。结果：

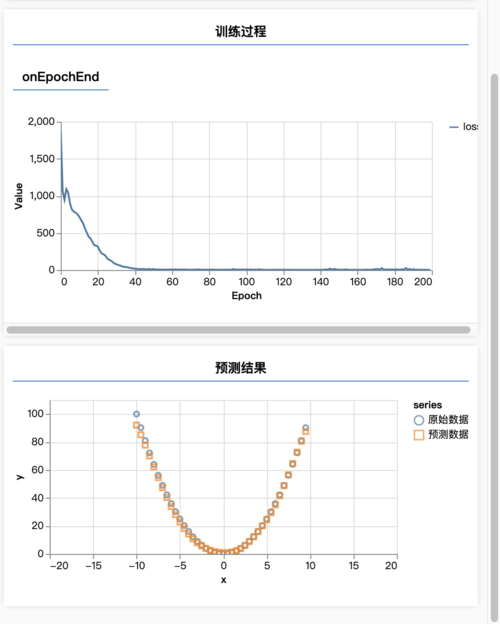
PS：这种问题几乎不会用神经网络来解，你应该找一些真实世界的数据来拟合。

0

1

二位取根

感谢老师！通过这次我有以下感悟：这种问题确实不适合用神经网络来解，x平方是一个固定值，并不需要去预测，去求解这个问题着实有点偏了。而且感觉这个预测效果和训练的数据有很大关系，比如老师这个代码对于0-1之间的平方预测出来的结果几乎就是完全错误的，大于给出数据范围的预测结果比如20也是完全不可参考的。我想如果将所有值都喂给机器去学习那么它的精准度可以大大提升，但就如上诉所说，这是完全没有必要的。通过老师的代码还是学习和验证了很多自己的想法！万分感谢！

2020-06-16

共1条回复

二位取根

提问者

2020-06-16

老师我还是不是很清楚，首先如果使用xor的模型的话，输出层的激活函数是sigmoid，高函数不是输出概率为0-1之间的吗？并且relu的曲线好像是抛弃了0以下的，不会有影响吗？其次我按照您说的换成了xor的模型使用平方的数据，但是还是没有想要的结果。我的理解是输出层激活函数还是应该使用均方误差，然后隐藏层使用其他的激活函数，归不归一化我都试过了（当然可能归一化理解错了），但是尝试过依旧不行，我将代码附上烦请您抽空帮我看看具体错在哪里，万分感谢。我感觉我还是没有理解到使用的真谛，只会单纯地理解您讲的。

import * as tf from '@tensorflow/tfjs';
import * as tfvis from '@tensorflow/tfjs-vis';
import { getData } from './data';

window.onload = async () => {
const data = getData(1000);
const xs = data.xArr;
const ys = data.yArr;

console.log('xs', xs);
console.log('ys', ys);

/*构造归一化训练数据*/
const xMin = Math.min.apply(null, xs);
const xMax = Math.max.apply(null, xs);
const yMin = Math.min.apply(null, ys);
const yMax = Math.max.apply(null, ys);

const inputs = normalizationData(xs, xMax, 0);
const labels = normalizationData(ys, yMax, 0);
console.log('inputs', inputs.dataSync());
console.log('labels', labels.dataSync());

/*将训练数据转换成tensor*/
/*   const inputs = tf.tensor(xs);
  const labels = tf.tensor(ys); */

/*
   * 归一化数据
   * */
function normalizationData(arr, max, min) {
return tf
.tensor(arr)
.sub(min)
.div(max - min);
}

/*
   * 反归一化
   * */
function unNormalizationData(output, max, min) {
return output
.mul(max - min)
.add(min)
.dataSync()[0];
}

/* 数据可视化 */
tfvis.render.scatterplot(
{
name: '非线性回归训练集',
},
{
values: xs.map((x, i) => ({
x,
y: ys[i],
})),
},
{
xAxisDomain: [-10, 10], // 设置x轴范围
yAxisDomain: [0, 100], // 设置y轴范围
}
);

/* 初始化模型 */
const model = tf.sequential(); // 连续模型(绝大多数问题都用这个)

/*添加隐藏层*/
model.add(
tf.layers.dense({
units: 4, // 神经元个数
inputShape: [1], // // 神经元(输入)接受的形状
activation: 'relu', // 这个激活函数可以带来一些非线性的变化，如果这里不要激活函数相当于这个隐藏层没有用，因为无论设置多少个层没有激活函数输出都是线性的
})
);

/*添加输出层*/
model.add(
tf.layers.dense({
// sequential为连续输出模型所以这里不需要设置inputshape
units: 1, // 只需要输出一个概率
activation: 'sigmoid', // 输出一个0-1的概率只能选sigmoid
})
);

/*新增损失函数和优化器*/
model.compile({
loss: tf.losses.logLoss,
optimizer: tf.train.adam(0.1),
});

/*异步训练模型*/
await model.fit(inputs, labels, {
validationData: [tf.tensor(xs), tf.tensor(ys)], // 验证集(格式和训练集一样)
batchSize: 200, // 每次样本需要学习的样本数据量
epochs: 100, // 训练轮数
callbacks: tfvis.show.fitCallbacks(
// 可视化模拟训练过程
{ name: '训练过程' },
['loss', 'val_loss', 'acc', 'val_acc'] // 训练集损失/验证集损失/训练集准确度/验证集准确度
),
});

$('#test')
.removeAttr('disabled')
.on('click', function () {
/*输出预测结果并显示*/
const output = model.predict(
normalizationData([Number($('#input').val())], xMax, 0)
/* tf.tensor([Number($('#input').val())]) */
); // 输入一个tensor帮你预测结果并赋值给变量
console.log('output', output.dataSync()[0]);
const resY = unNormalizationData(output, yMax, 0);
/* const resY = output; */
console.log('output', resY);
});
};

数据代码：

export function getData(numSamples) {
let xArr = [];
let yArr = [];
let count = 0;

for (let i = 0; i < numSamples - 1; i++) {
count += 1; // 可调
xArr.push(count);
yArr.push(count * count);
xArr.push(-count);
yArr.push(count * count);
}
let data = {
xArr: xArr,
yArr: yArr,
};
console.log('data', data);
return data;
}

0

0

二位取根

提问者

2020-06-15

老师您好，多层神经网络的课程我已经看完。给我的感觉是照着您的代码学，也是能够理解，跟着敲也能正确，但是就是不能够很好的举一反三。比如我又尝试了那个求平方的问题，就很迷茫，损失函数使用什么？是否是均方误差？激活函数应该用什么？应该用几层？等等，我尝试了两层添加激活函数，也试过将数据归一化再处理，但是都得不到很好的结果，望老师指点一二

0

1

lewis

你把xor的网络换成平方的数据，就可以很好拟合

2020-06-15

共1条回复

lewis

2020-06-11

看到后面你就知道，多层神经网络可以拟合任何复杂的非线性问题

0

0