1回答

liuyubobobo

2023-03-28

非常非常重要的，我在这个课程说过“看待矩阵的四个视角”，不是矩阵乘法对象的改变（和你写的四个视角完全不同。）我总结的“看待矩阵的四个视角”，本质可以理解成对于矩阵的最典型的四种应用：数据，系统，变换，空间：

你描述的，不是看待同一个东西的四种视角。你描述的，完全不是一个东西。

向量和向量之间定义了点乘，所以，(2, 1) 这个向量点乘 (3, 5) 这个向量，结果是 2 * 3 + 1 * 5 = 11。注意，两个向量的点乘结果是一个数字！

在学习了矩阵运算以后，我们可以看到，我们使用 （2， 1） 行向量和 (3, 5) 列向量可以做矩阵乘法，但此时，这个乘法和上面的 (2, 1) 和 (3, 5) 两个向量做点乘是不一样的。 （2， 1） 行向量和 (3, 5) 列向量做矩阵乘法，本质是 (2, 1) 这样的一个 1 * 2 的矩阵；和 (3, 5) 列向量（即 2 * 1 的矩阵）做矩阵乘法，结果是 （11），结果是一个矩阵！只不过这个矩阵是一个 1*1 的矩阵而已。两个矩阵乘法的结果不是一个数字，而是一个矩阵！（相应的，两个响亮的乘法结果是一个数字，不是一个矩阵。）

在这个描述中，当我说 (3, 5) 列向量的时候，其实已经将 (3, 5) 看做是一个矩阵了，因为向量本身是没有方向的。向量就是一串数字。矩阵才有方向，所以矩阵才可以做转置运算，向量没有转置运算。（一个数组你横着看竖着看都不重要，斜着看也行，数组就是一串有序数字。）

明白了这一点，再看为什么 （2， 1）列向量和 (3, 5) 行向量做矩阵乘法，结果是 2*2 矩阵，就很明显了。因为此时其实是 (2, 1) 列向量，这个 2 * 1 的矩阵，和 (3, 5) 行向量，这个 1*2 的矩阵，再做矩阵乘法。根据矩阵乘法的定义，得到了一个 2*2 的矩阵。这一切和上面的  （2， 1） 行向量和 (3, 5) 列向量做矩阵乘法，规则是一致的，只不过因为矩阵乘法没有交换律，所以结果不同而已，但他们都是矩阵乘法！（相应的，向量之间的点乘是支持交换律的。）

最后，矩阵和向量之间的运算，一个矩阵和一个向量之间可以做乘法运算，但要要求矩阵的列数和向量的元素数一致，结果是一个向量。注意，结果是一个向量！不是另一个矩阵！所以，我在课程中说，这个运算可以理解成是向量转换的函数（从一个向量转换成另一个向量）：

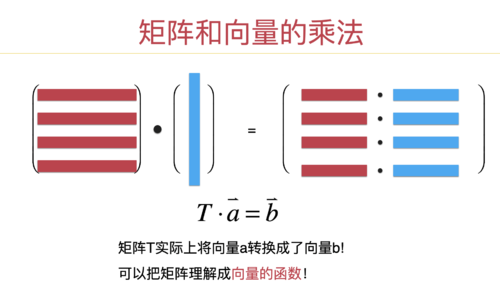
但是，你可以把上面图市里的“列向量”，看做是 m * 1 的矩阵，此时，就变成了矩阵和矩阵的乘法，但注意，此时结果是一个矩阵！（只不过一个维度为 1 而已。）

一个向量和一个矩阵是不能运算的。但是，如果我们把向量看做是一个 1 * n 的矩阵的话，是可以和一个 n * m 的矩阵运算的，但此时，他们的结果是一个 1 * m 的矩阵，而非一个含有 m 个元素的向量！（因为矩阵和矩阵乘法的结果是矩阵！）

说来说去，就是：数，向量，矩阵，不是一个概念。但很多时候，我们做了一些“隐式”的转换，尤其是对于向量的处理上，其实是把向量看做了一个矩阵。

说成计算机的语言，就是：

一个数组中只包含一个数字，他还是一个数组，不是一个数字；（一个含有一个元素的向量，不是一个数字）

一个二维数组，其中一个维度为 1，他还是一个二维数组，不是一个一维数组（一个矩阵，即使一个维度为 1，还是一个矩阵，不是一个向量）。

在这样的概念前提下，向量和向量之间；矩阵和向量之间；矩阵和矩阵之间，定义了他们之间的乘法运算。这些乘法运算是不一样的，虽然在一些情况下，我们可以把数组做“类型转换”，然后去做“别的运算”（比如把向量转换成某一个维度为 1 的矩阵，然后去做矩阵运算），但你一定要明白在底层，到底什么什么类型和什么类型再做运算。

希望我讲明白了。

继续加油！：）

0

1

慕设计1008376

哇噢，感谢bobo老师的回复！值得我细细反复品读。 另外，求更新微积分和概率论数理统计相关的课程，再次感谢！

2023-03-28

共1条回复