n阶矩阵有n个特征值
来源:13-5 “不简单”的特征值

江景又妍和
2019-07-23
bobo老师,我今天看线代课本,有一个默认的结论说,如果说A是n维矩阵,那么它对应的特征值有n个。这个结论我想了一下您之前所说的一个特征值就对应一个特征空间,然后没有想明白这里的是指对应于n个特征空间吗? 为什么这个n维的变换矩阵会对应n个特征空间呢?老师可以从几何的层面讲解一下嘛,感觉这样会更容易理解。麻烦老师啦(*°∀°)=3
2回答
-
1.
首先,为什么A是n维方阵,对应特征值有n个?
因为,我们求解特征值的方法,即特征方程:det(A-λI) = 0,一定是一个关于λ的n次方程!所以,λ有n个解。(但有可能有重复解或者复数解)
以下是第2小节ppt截图:

2.
为什么每一个特征值就对应一个特征空间?
所谓的特征空间,就是特征向量(加零向量)组成的空间。因为每一个特征值对应一组特征向量,所以每一个特征值自然对应一组特征空间。
这里的关键,其实是:凭什么一个特征值对应的一组特征向量,形成了向量空间?(注意:向量空间是有条件的,及课程中介绍的对向量加法和点乘封闭)
答案是:根据特征向量求解的式子,我们能看到,特征向量就是A-λI的零空间。(这里用到了零空间的定义。)
以下是第2小节ppt截图:

3.
几何解释
特征值和特征空间就是比较抽象。尤其是在有重根和复数根的情况下。
这一章后续,介绍的矩阵对角化,可以看作是对如果A有n个线性无关的特征向量的话,对应的一个几何解释。
因为根据可对角化的原理,如果A有n个线性无关的特征向量,则A一定和这样一个D相似:

将矩阵相似性的时候,我一直强调相似型的一个几何含义:即A和B相似,代表A和B是同样的变换,只是观察坐标系不同。

那么,上面的A可以对角化,就说明,A和D本质是一样的。但是,D就是一个正交矩阵。它表示的变换,知识在各个坐标轴上缩放一个倍数而已。所以,A变换,本质就是D这个变换,也就是在各个维度缩放了特征值大小这么多倍!
但是,这里没有考虑旋转,旋转是被矩阵P定义的,而矩阵P是有由特征向量构成的。
由于A有n个线性无关的特征值,所以A的n个特征向量空间一定是1维的(回忆一下:几何重数等于代数重数)
换句话说,每一个特征向量空间,就是一个坐标轴!(这可能就是你要的几何解释)
因此,所有的特征向量构成的矩阵,就是对原矩阵A进行一个坐标转换,转换后,A就变成了一个D这样简单的变换。
这里,还要再融会贯通一下相似性的这个图:
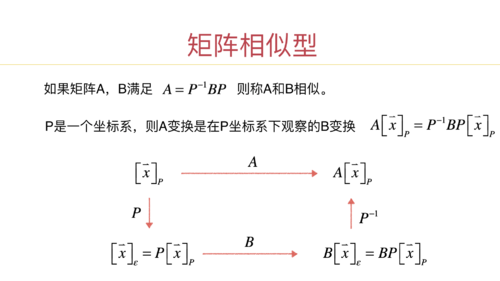
当然,这里只是对A有n个不同的特征向量的情况做的说明。
如果A的特征值有重根或者复数,理解起来就更复杂了。印象课程中说过,我们在这个课程中不考虑这些情况。(我印象里听同学说过,考研中似乎也不会应用有重根的特征值?最多是求解?)
加油!:)
012019-07-24 -

江景又妍和
提问者
2019-07-23
对了,老师这里所说的n个特征值包括重根,即一个二重根看做两个特征值
00





